求i等于多少,需要具体步骤!!!
发布时间:2019-08-08 00:15:56
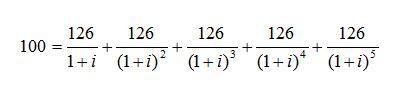
推荐回答
还没有选出推荐答案,请稍候访问或查看其他回答!其他回答
具体步骤
令 1/(1+ i) = a, 则 a + a^2 + a^3 + a^4 + a^5 = 100/126;①
左边是等比级数, a + a^2 + a^3 + a^4 + a^5 = a( a^5 - 1 )/( a - 1 )
故 ( a^6 - a )/ ( a - 1 ) = 100/126,126a^6 - 226a + 100 = 0
解方程 a1 = 1,代入 ①,不成立,是增根;
a2 = 0.446920546,代入①,成立;
i = 1/a - 1 = 1.237534185774488873 。
100(1+i)∧5=126[(1+i)∧4+(1+i)∧3+(1+i)∧2+(1+i)+1]
等差数列求和公式,我忘了,自己算吧
原式变形100/126=1/(1+i)+1/(1+i)²+1/(1+i)³+1/(1+i)四次方+1/(1+i)五次方
100/126=【(1+i)四次方+(1+i)³+(1+i)²+1】/(1+i)五次方,
126=(1+i)五次方
i=(126)开五次方-1
以上问题属网友观点,不代表本站立场,仅供参考!
- 上一条:一只电炉的电阻和一台电动机的
- 下一条:李大伯用64米的篱笆围一块长方