设函数f(x)=a为常数且a∈(0,1).(1)当a=时,求f;(2)若x0满足f[f(x0)]=x0,但f(x0)≠x0,则称x0为f(x)的二阶周期点.证明函数f(x)有且仅有两个二阶周期点,并求
发布时间:2019-08-08 02:54:26
试题难度:难度:偏难 试题类型:解答题 试题内容:设函数f(x)=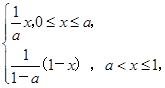 a为常数且a∈(0,1).
a为常数且a∈(0,1).
(1)当a=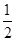 时,求f
时,求f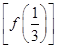 ;
;
(2)若x0满足f[f(x0)]=x0,但f(x0)≠x0,则称x0为f(x)的二阶周期点.证明函数f(x)有且仅有两个二阶周期点,并求二阶周期点x1,x2;
(3)对于(2)中的x1,x2,设A(x1,f[f(x1)]),B(x2,f[f(x2)]),C(a2,0),记△ABC的面积为S(a),求S(a)在区间[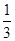 ,
,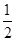 ]上的最大值和最小值.
]上的最大值和最小值.
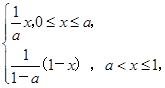 a为常数且a∈(0,1).
a为常数且a∈(0,1).(1)当a=
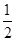 时,求f
时,求f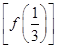 ;
; (2)若x0满足f[f(x0)]=x0,但f(x0)≠x0,则称x0为f(x)的二阶周期点.证明函数f(x)有且仅有两个二阶周期点,并求二阶周期点x1,x2;
(3)对于(2)中的x1,x2,设A(x1,f[f(x1)]),B(x2,f[f(x2)]),C(a2,0),记△ABC的面积为S(a),求S(a)在区间[
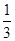 ,
,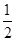 ]上的最大值和最小值.
]上的最大值和最小值.推荐回答
还没有选出推荐答案,请稍候访问或查看其他回答!以上问题属网友观点,不代表本站立场,仅供参考!
- 上一条:问题情境已知矩形的面积为a(a为
- 下一条:已知函数,其中a为常数.(1)当时,求的